PythonでFuzzy C-meansクラスタリング

この記事に書かれていること

Fuzzy C-meansについて
PythonによるFuzzy C-meansの実装

Fuzzy C-meansクラスタリングとは

Fuzzy C-meansクラスタリングとは、前回記事に書いたK-meansと似た非階層型クラスタリングの１つです。

PythonでK-meansクラスタリング - 理系大学生がPythonで色々頑張るブログ

K-meansはベクトル間距離と、クラスタ数を設定する事でクラスタリングを行う事が出来ました。
また、対象のベクトルに対し、最も近接した重心ベクトルを所属クラスタとしていました。

C-meansは対象のベクトルに対し、それぞれのクラスタへの所属度というパラメータで、各クラスタに対してどれくらい近いかを求めます。
クラスタが一意に決定するK-meansに対し、複数のクラスタへの所属を許すFuzzyなクラスタリングとなります。

アルゴリズム

特徴ベクトルの集合を、クラスタを、クラスタへの所属度、クラスタの重心、ファジィパラメータとした時、fuzzy C-meansのアルゴリズムは次のようになります。

1. 所属度をランダムに初期化

2. 各クラスの重心ベクトルを計算

3. 全ての特徴ベクトルに対し、各クラスタへの所属度を更新

はユークリッド距離を表しています。

4. の変化が十分に小さくなれば終了。そうでなければ2に戻る。

PythonによるFuzzy C-meansクラスタリングの実装

__author__ = 'emoson'
import numpy as np


def near(x, mu, m):
    """特徴ベクトルの各クラスタへの所属度を返す"""
    return [np.sum([(np.linalg.norm(x-mu[k])/np.linalg.norm(x-mu[j]))**(2/(m-1)) for j in range(mu.shape[0])])**-1 for k in range(mu.shape[0])]


def clustering(X, K=3, m=1.5):
    """
    Fuzzy C-meansクラスタリング
    X: 特徴ベクトルの集合
    K: クラスタ数
    m: Fuzzyパラメータ
    """
    #データ総数
    N = len(X)
    #前ステップの重心
    old_mu = np.array([K, N])
    #寄与度
    u = np.random.random([K, N])
    e = np.inf
    while True:
        #重心の算出
        mu = np.dot(u, X)/np.array([np.sum(u, axis=1)]).T
        #寄与度の更新
        for k in range(K):
            for i in range(N):
                u[k, i] = np.sum([(np.linalg.norm(X[i]-mu[k])/np.linalg.norm(X[i]-mu[j]))**(2/(m-1)) for j in range(K)])**-1
        _e = np.linalg.norm(mu-old_mu)
        if _e > e:break
        e = _e
    return mu

次の様に実行します。

#学習する特徴ベクトル数
N = 100
#特徴ベクトルの集合
X = np.random.random([N, 2])
#Fuzzyパラメータ
m = 2.0
#クラスタリング
mu = clustering(test_X, K, m)
#各クラスタへの所属度を求める
near([0.1, 0.3], mu, m)

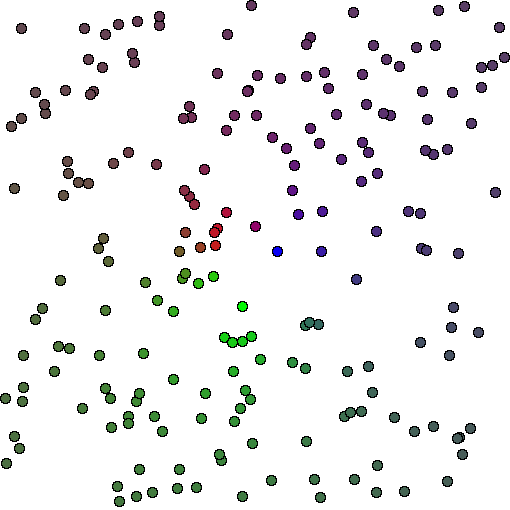
X,Y平面上に特徴点をランダムにプロッティング、クラスタ数を3でクラスタリングし、クラスタの所属度に応じて色を塗り分けると次のようになりました。
複数のクラスタの間にプロットされた特徴点の色がグラデーションになっており、所属クラスタがFuzzyにも止まっていることがわかります。